SCIENCE
It has long been theorized that two stars can come together and merge. Our best evidence that such an event can occur is variable star V1309 Sco, which exploded in 2008. However, no theoretical model could successfully predict the light curve.
I was among the first to successfully recreate the V1309 Sco light curve during the plateau and subsequent gradual dimming. I used a Smoothed Particle Hydrodynamics (SPH) code called StarSmasher to model the stars as fluids. I introduced a novel implementation of flux-limited radiative diffusion to StarSmasher to calculate the emitted light and compared the result to the V1309 Sco light curve.
Hatfull, R. W. M. & Ivanova, N., 2024, ApJ, Accepted, doi: 10.48550/arXiv.2412.06583
Hatfull, R. W. M., 2024. Simulating a Stellar Contact Binary Merger. PhD Thesis. University of Alberta.
Hatfull, R. W. M., 2019. Solving the radiative transfer problem in SPH simulations of contact binary mergers using FluxCal. MSc Thesis. University of Alberta. doi: 10.7939/r3-j6xb-2x88
Hatfull, R. W. M., Ivanova, N., & Lombardi, J. C., 2021, MNRAS, 507, 385, doi: 10.1093/mnras/stab2140
Wenskovitch J. E., Lombardi J. C., Hatfull R. W. M., 2016, in SIGGRAPH Asia 2016 Symposium on Visualization. SA ‘16. Association for Computing Machinery, New York, NY, USA, doi: 10.1145/3002151.3002154
Warning
You are now entering nerd territory.
The content below might be a bit dry, but there is a funny video at the end and the jokes might not make sense unless you read this stuff first.
There’s pretty pictures along the way!
Stellar Mergers
Since antiquity, astronomers have been fascinated by pairs of stars that appear close to each other on the sky, some of which can be bound gravitationally in a shared orbit (Michell, 1767), called a “binary”. A binary can form when dense clouds of molecular gas in the interstellar medium collapse under self-gravity to form either a single star or fragment to form a collection of stars (McKee and Ostriker, 2007). Although the underlying mechanisms for this fragmentation are unclear, both wide and close binary systems have been observed after a protostellar core collapse, with more than ~50% of Sun-like stars having stellar companions (Raghavan et al., 2010), 10-15% of which have separations of only a few Earth-Sun distances. More than 80% of stars with masses > 16 M are in a binary (Duchêne and Kraus, 2013). When one of the stars in such a binary eventually evolves off the main sequence and onto the red giant branch, its envelope expands. The expanded star, called the “donor” (also called the “primary” star), can eventually transfer mass to the other star, called the “companion” (also called the “secondary” star).
Figure 1: A 3D sketch of the effective gravitational potential field 𝜑 (gray) offset from two point masses. I show lines of equipotential corresponding to the first three Lagrange points, 𝐿1 (blue), 𝐿2 (orange), and 𝐿3 (green).
To understand the evolution, consider the stars as point masses in a shared orbit with orbital frequency 𝜔. The net gravitational force acting on a small packet of mass 𝑚 is 𝐹 = −𝑚∇𝜑, where the effective gravitational potential
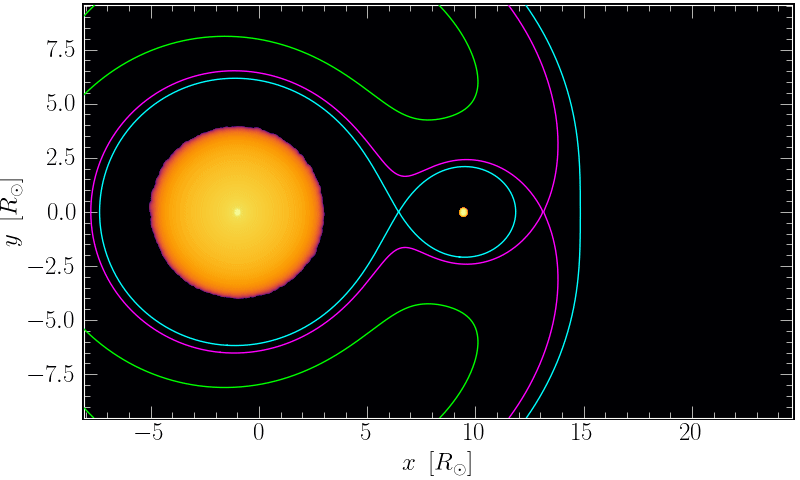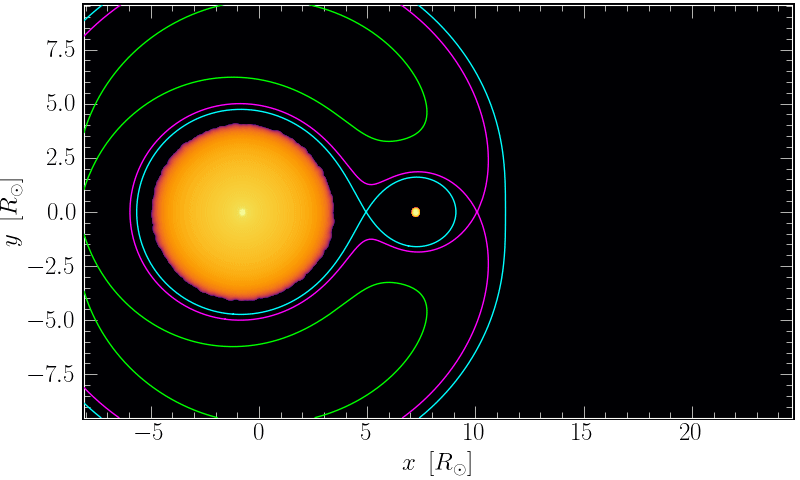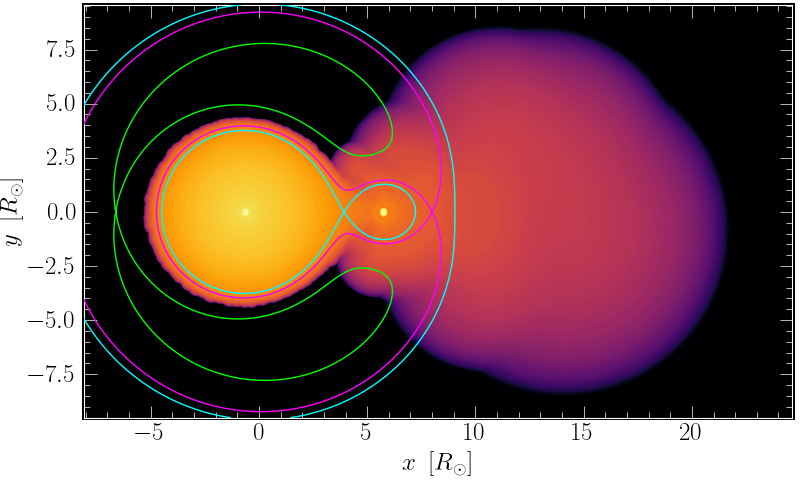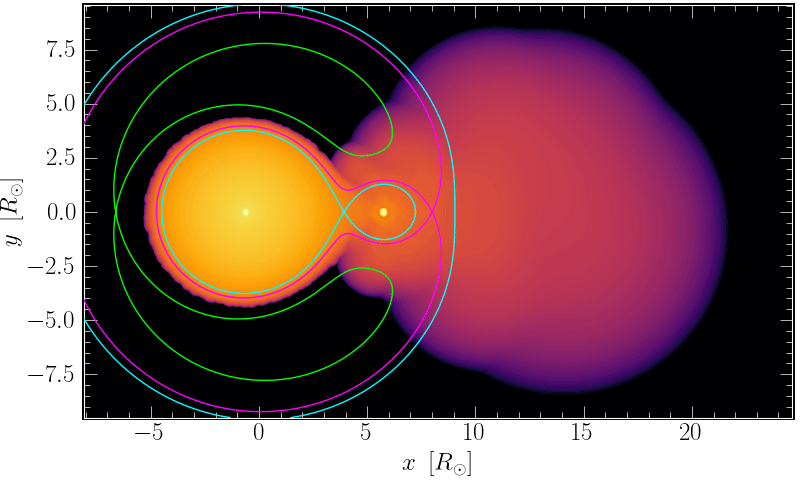
The three local maxima in 𝜑 define the Lagrange points 𝐿1, 𝐿2, and 𝐿3, as shown in Figure 1. During the binary interaction, mass begins to fill a region called a Roche lobe (RL), which is a volume surrounding each star defined by the 𝐿1 equipotential. Once a star has filled its RL, mass transfer can proceed around 𝐿1 and mass can also overflow into the volume defined by 𝐿2. As shown in Figure 2, matter can eventually leave the system as streaming ejecta through 𝐿2 and 𝐿3, which further removes angular momentum from the binary’s orbit. The process can culminate with the companion plunging into the donor’s envelope.
Figure 2: An example Smoothed Particle Hydrodynamics (SPH) simulation showing the log column density as two stars in a binary undergo a shrinking orbit, in a corotating reference frame. I show the equipotential lines corresponding with the Lagrange points 𝐿1 (blue), 𝐿2 (purple), and 𝐿3 (green). Mass transfers from the donor to the companion through 𝐿1. The companion’s Roche lobe is quickly filled, and outflow begins through 𝐿2. Created using starsmashertools.
This process is often described in the literature as a common envelope (CE) event (Paczynski, 1976). A multitude of astrophysical phenomenon have been explained by CE events, such as: X-ray binaries (van den Heuvel, 1976), binary pulsars (Smarr & Blandford, 1976), cataclysmic variables, close double white dwarf binaries, Type Ia supernovae progenitors (Iben & Livio, 1993), hot subdwarfs (Han et al., 2002), blue and red stragglers (McCrea, 1964; Ferreira et al., 2019; Britavskiy et al., 2019), gravitational wave source progenitors (Tutukov & Yungelson, 1979), and blue lurkers (Leiner et al., 2019; Sun et al., 2024).
Britavskiy, N., Lennon, D. J., Patrick, L. R., et al. 2019, A&A, 624, A128, doi: 10.1051/0004-6361/201834564
Duchêne, G., & Kraus, A. 2013, Annual Review of Astronomy and Astrophysics, 51, 269, doi: 10.1146/annurev-astro-081710-102602
Ferreira, T., Saito, R. K., Minniti, D., et al. 2019, MNRAS, 486, 1220, doi: 10.1093/mnras/stz878
Han, Z., Podsiadlowski, P., Maxted, P. F. L., Marsh, T. R., & Ivanova, N. 2002, MNRAS, 336, 449, doi: 10.1046/j.1365-8711.2002.05752.x
Iben, Jr., I., & Livio, M. 1993, PASP, 105, 1373, doi: 10.1086/133321
Leiner, E., Mathieu, R. D., Vanderburg, A., Gosnell, N. M., & Smith, J. C. 2019, ApJ, 881, 47, doi: 10.3847/1538-4357/ab2bf8
McCrea, W. H. 1964, MNRAS, 128, 147, doi: 10.1093/mnras/128.2.147
McKee, C. F., & Ostriker, E. C. 2007, Annual Review of Astronomy and Astrophysics, 45, 565, doi: 10.1146/annurev.astro.45.051806.110602
Michell, J. 1767, Philosophical Transactions of the Royal Society of London Series I, 57, 234
Paczynski, B. 1976, in IAU Symposium, Vol. 73, Structure and Evolution of Close Binary Systems, ed. P. Eggleton, S. Mitton, & J. Whelan, 75
Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, The Astrophysical Journal Supplement Series, 190, 1, doi: 10.1088/0067-0049/190/1/1
Smarr, L. L., & Blandford, R. 1976, ApJ, 207, 574, doi: 10.1086/154524
Sun, M., Levina, S., Gossage, S., et al. 2024, ApJ, 969, 8, doi: 10.3847/1538-4357/ad47c1
Tutukov, A., & Yungelson, L. 1979, in IAU Symposium, Vol. 83, Mass Loss and Evolution of O-Type Stars, ed. P. S. Conti & C. W. H. De Loore, 401–406
van den Heuvel, E. P. J. 1976, in Structure and Evolution of Close Binary Systems, ed. P. Eggleton, S. Mitton, & J. Whelan, Vol. 73, 35
V1309 Sco
Figure 3: Infrared (I-band) light curve of V1309 Sco, with an inset plot of the orbital period leading up to the outburst. “JD” stands for “Julian Days”. Adapted from Tylenda et al. (2011).
In 2008, variable star V1309 Sco exploded, producing the light curve shown in Figure 3. Within a year, it went from being about as bright (in the infrared) as Pluto to nearly visible to the naked eye. For several weeks thereafter, it maintained the same brightness before gradually dimming over the next several years. Archival data revealed that there were two stars locked in an orbit with each other, and that the orbit was exponentially shrinking. Now considered a landmark observation, the case of V1309 Sco presents some of the strongest evidence that two stars can come into contact and merge — an idea originally proposed in the 1970’s. However, the fate of the two stars in V1309 Sco is still unknown, as they remain shrouded in dust to this day.
V1309 Sco is the poster child for a recently identified category of events called Luminous Red Novae (LRNe), about which there are still many unanswered questions, such as:
Are stellar mergers the sole cause LRNe? Can a stellar collision create an LRN?
Why is there a plateau in brightness? If the stars were different, how would the light curve change?
What remains of the stars after the explosion? Is one star left, or two stars with a tighter orbit?
What signs should we look for when an LRN is about to happen?
Funny Video
(as promised)
🚨 CAUTION 🚨
NERD ZONE INTENSIFYING
Proceed only if you consider yourself to be either a finite fluid element, or a functional from the space of all continuous, infinitely differentiable linear functionals. You have been warned.
Smoothed Particle Hydrodynamics (SPH)
The SPH method is a popular technique in which the fluid continuum is reconstructed by interpolating over individual mass elements called particles (Lucy, 1977; Gingold & Monaghan, 1977). The SPH method can be understood by letting any property of a physical fluid can be described by a continuous function 𝐴(𝑟), where 𝑟 is a 3D position. Following chapter 1 of Gel’fand (1964), all real functions 𝜑(𝑟) with continuous derivatives of all orders and with “compact support” (the value of the function is zero everywhere except within some bounded region) can be associated with a generalized functional (𝐴, 𝜑):
where the integral is taken only over the bounded region. One common application of the above equation is the well-known Dirac 𝛿 identity:
where I have let the fluid be heterogeneous, such that the density ρ(𝑟) = 𝑑𝑚(𝑟)/𝑑𝑉.
The above equation describes the distribution of singular fluid elements, each of mass 𝑑𝑚 and volume 𝑑𝑉, located at 𝑟′, such that 𝐴(𝑟′) ≠ 0. Thus, it implies that the fluid consists of an infinite number 𝑁 → ∞ of infinitesimally small elements. However, to conduct a computer simulation, only a finite 𝑁 can be used, and so some function other than the Dirac 𝛿 must be chosen for 𝜑(𝑟). During the discretization process, most of the elements in the original, physical fluid are “removed”, leaving a sufficiently small 𝑁 remaining for computations. This means that after discretization, there exist locations where formerly 𝐴(𝑟′) ≠ 0, but now 𝐴(𝑟′) = 0.
The SPH method reconstructs the 𝐴(𝑟′) values that were lost during discretization by “broadening” the Dirac 𝛿 (Lucy, 1977), replacing it with some other function 𝑊 (|𝑟 − 𝑟′|, ℎ) of compact support ℎ, called a “kernel function”:
where 𝑖 represents element 𝑖, 𝑁nb,𝑖 is the number of “neighboring” elements 𝑗 that are used in the interpolation, and ℎ is the “smoothing length”, defining the compact support of kernel function 𝑊. The smoothing length ℎ is dynamically adjusted for each SPH particle to control the interpolation properties, in a manner that usually depends on the specific SPH implementation.
Figure 4: The “smoothing” action in Smoothed Particle Hydrodynamics works by broadening the Dirac 𝛿 by replacing it with a different linear functional from the same mathematical space as 𝛿.
The SPH method can be understood as a weighted sum interpolation. In the case of the Dirac 𝛿 formulation, it is 𝛿 that provides the weights, and ∫ 𝛿(|𝑟 − 𝑟′|)𝑑𝑟′ = 1. In the case of 𝑊 supplying the weights, as in the equation above, ∫ 𝑊 (|𝑟 − 𝑟′|, ℎ)𝑑𝑟′ = 1. To preserve continuity in 𝑊, the function must also satisfy the condition 𝑊 → 𝛿 as ℎ → 0, which is equivalent to 𝑊 → 𝛿 as 𝑁 → ∞.
The physical meaning of 𝑊 is a common source of confusion. In addition to the previously mentioned requirements, 𝑊 can be any continuous linear functional that converges uniformly in a bounded region (compact support) and has continuous derivatives of all orders. The most important consequence is that 𝑊 has no physical meaning; it is simply one of the properties of SPH interpolation. Although it is true that the physical fluid does exist somewhere within the volume surrounding each fluid element defined by ℎ (called a “kernel”), it is impossible to accurately reconstruct the fluid properties anywhere other than directly at the location of a particle. That is, it is possible for 𝐴(𝑟) = 0 within the kernels, and also for 𝐴(𝑟) ≠ 0 in places where no actual fluid existed before the discretization step.
The SPH method has been widely used to simulate stellar mergers, though only a few include radiative transfer models (Pejcha et al., 2016; Metzger & Pejcha, 2017; Pejcha et al., 2017), and none produced a light curve of the full evolution.
Gel’fand, I. M. 1964, Generalized functions. (Academic Press Inc.). https://login.ezproxy.library.ualberta.ca/login?url=https://search.ebscohost.com/login.aspx?direct=true&db=cat03710a&AN=alb.7404129&site=eds-live&scope=site
Gingold, R. A., & Monaghan, J. J. 1977, MNRAS, 181, 375, doi: 10.1093/mnras/181.3.375
Lucy, L. B. 1977, AJ, 82, 1013, doi: 10.1086/112164
Metzger, B. D., & Pejcha, O. 2017, MNRAS, 471, 3200, doi: 10.1093/mnras/stx1768
Pejcha, O., Metzger, B. D., & Tomida, K. 2016, MNRAS, 461, 2527, doi: 10.1093/mnras/stw1481
Pejcha, O., Metzger, B. D., Tyles, J. G., & Tomida, K. 2017, ApJ, 850, 59, doi: 10.3847/1538-4357/aa95b9